Computational mechanics of
structures and materials

Fracture is one of the most commonly encountered failure modes of engineering materials and structures. The prevention of fracture-induced failure is, therefore, a major constraint in engineering designs. As with many other physical phenomena computational modelling of fracture constitutes an indispensable tool not only to predict the failure of cracked structures but also to shed insights into the mechanism of the fracture processes of many materials such as concrete, rock, ceramic, metals and biological soft tissues. The subject has been extensively studied since the milestone work of Griffith [1920] and Irwin [1957] who established the field of fracture mechanics with their theory of linear elastic fracture mechanics (LEFM). Still, predictive modelling of crack propagation remains one of the most significant challenges in solid mechanics.
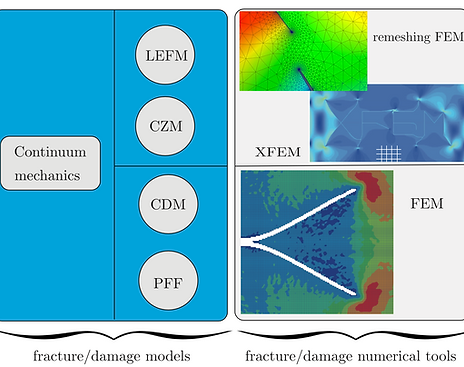
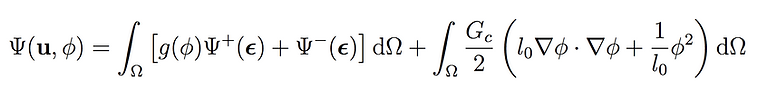
Phase field approach to modelling fracture is a relatively new method, which attracts interests of many researchers due to ist capability (1) to handle initiation/propagation/merging/branching of cracks in both 2D and 3D with a relatively straightforward computer implementation, and (2) to model multiple physics in a straightforward manner. According to this method, a continuous field ranging from 0 to 1 is used to differentiate the intact material and the damaged one. The displacement field and the phase field is sought to minise an energy functional, which is written as follows for brittle fracture:

where the first integral denotes the decreasing strain energy (due to damage evolution) and the second integral is the Griffith surface energy, which is an increasing quantity due to damage growth.
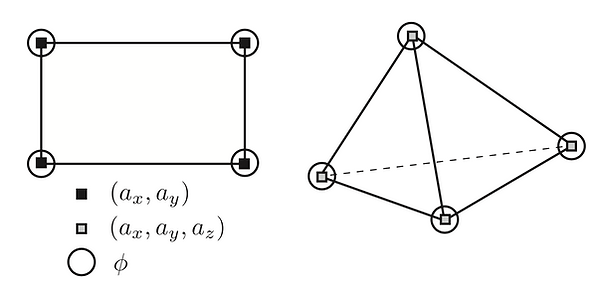
This phase field fracture model can be implemented with ease using the so-called multi-field finite elements where at each node in addition to the standard displacement degrees of freedom (dof) one now has the scalar phase field dof. If a monolithic solver is used, the resulting discrete equations are very similar to the ones of the gradient-enhanced damage model of Peerling et al, even though no damage widening is happening.

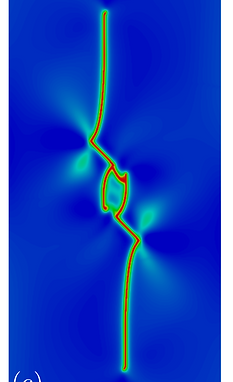
Phase field fracture simulations using a monolithic solver are, however, not robust probably due to the non-convexity of the energy functional. Therefore, in practice, the so-called alternating minimisation (AM) solver (also referred to as staggered solver) is usually adopted. In this solver, one solves two sub-problems: the displacement problem with the phase field fixed and the phase field problem with the displacement field fixed. This solver is implemented in jive (https://jive.dynaflow.com). And some quasi-static and dynamics brittle fracture simulations are conducted and shown below.
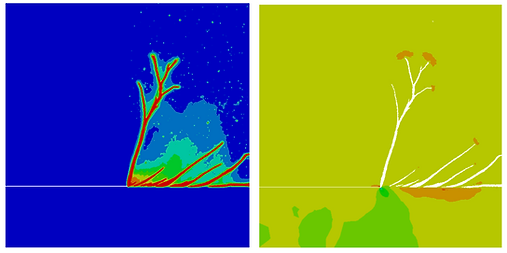
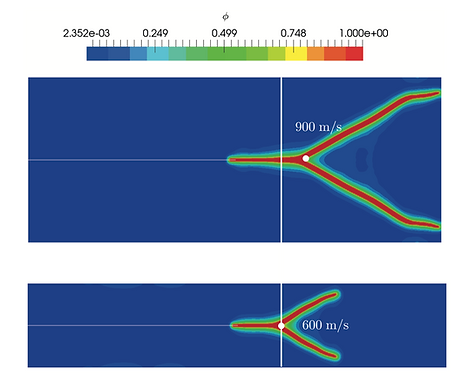
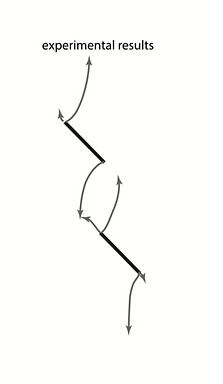
Two well known dynamics fracture problems are solved using a PFF model. On the left figure, is shown the dynamic crack branching with different imposed velocities. And on the right figure, is shown the Kalthoff experiment with a large impact velocity of 100 m/s. As can be seen, multiple dynamic crack branching can be captured.

References
-
B. Bourdin, G.A. Francfort, and J-J. Marigo. Numerical experiments in revisited brittle fracture. Journal of the Mechanics and Physics of Solids, 48(4):797 – 826, 2000
-
J. Y. Wu. A unified phase-field theory for the mechanics of damage and quasi-brittle failure. Journal of the Mechanics and Physics of Solids, 103:72 – 99, 2017. pdf
-
V.P. Nguyen, D. Sutulas, S. Bordas and Y. Lu . Computational modelling of multiple crack growth: a comparison between discrete and phase field models. 9th Australian Conference on Applied Mechanics, UNSW, Sydney, 2017. pdf
-
J.Y. Wu, V.P. Nguyen. A length scale insensitive phase-field damage model for brittle fracture. Journal of the Mechanics and Physics of Solids, 2018. pdf
-
V. P. Nguyen and J. Y. Wu. Modeling dynamic fracture of solids with a phase-field regularized cohesive zone model. Computer Methods in Applied Mechanics and Engineering, 2018. pdf
-
J. Y. Jian, J. F. Qiu, V. P. Nguyen, T. K. Mandal and L. J. Zhuang. Computational modeling of localized failure in solids: XFEM vs PF-CZM. Computer Methods in Applied Mechanics and Engineering, 2018. pdf
-
T. K. Mandal, V. P. Nguyen, and A. Heidarpour. Phase field and gradient enhanced damage models for quasi-brittle failure: a numerical comparative study. Engineering Fracture Mechanics, 2018. link.
-
Nguyen, N.-H., Nguyen, V. P., Wu, J.-Y., Le, T.-H.-H., Ding, Y., 2019. Mesh based and meshfree reduced order phase-field models for brittle fracture: One dimensional problems. Materials 12, 1858. link
-
T. K. Mandal, V. P. Nguyen and J. Y. Wu, 2019. Length scale and mesh bias sensitivity of phase-field models for brittle and cohesive fracture. Engineering Fracture Mechanics. link
-
J. Y. Wu, V. P. Nguyen, H Zhou and Y. Huang 2019. A variationally consistent phase-field anisotropic damage model for fracture. Computer Methods in Applied Mechanics and Engineering. link.
-
J. Y. Wu, T. K. Mandal and V. P. Nguyen, 2019. A phase-field regularized cohesive zone model for hydrogen assisted cracking. Computer Methods in Applied Mechanics and Engineering . link.
-
J.Y. Wu, Y. Huang, H. Zhou and V.P .Nguyen, 2020. Three-dimensional phase-field modeling of mode I + II/III failure in solids. Computer Methods in Applied Mechanics and Engineering. link
-
T. K. Mandal, V. P. Nguyen and J. Y. Wu, 2020. A length scale insensitive anisotropic phase field fracture model for hyperelastic composites, International Journal of Mechanical Sciences. link
-
T. K. Mandal, V. P. Nguyen and J. Y. Wu, 2020. Evaluation of variational phase-field models for dynamic brittle fracture. Engineering Fracture Mechanics. link.
-
T. K. Mandal, A. Gupta, V. P. Nguyen, R. Chowdhury and A, de Vaucorbeil 2020. A length scale insensitive phase field model for brittle fracture of hyperelastic solids. Engineering Fracture Mechanics. link.
-
J. Y. Wu, V. P. Nguyen, H Zhou and Y. Huang 2019. On the BFGS monolithic algorithm for the unified phase field damage theory. Computer Methods in Applied Mechanics and Engineering. link.