top of page
This site was designed with the
.com
website builder. Create your website today.Start Now

When doing a finite element analysis (or any other numerical PDE solvers) of a structure one usually needs a constitutive model that describes the (mechanical) behaviour of the material from which the structure is made. These materials are macroscopically homogeneous but microscopically heterogeneous. Most of the time, constitutive models are (1) closed form, (2) phenomenological and (3) require many parameters that are even non-measurable (for very complex behaviours).

​

Computational homogenisation (CH) is a method within the so-called multiscale material modelling framework that allows the modelling of material behaviour at large scales based on information obtained from lower scales. That is, the microstructure (e.g. aggregates in concrete) and its evolution can be taken into account.  Note that CH can be classified into two categories: semi-concurrent methods (also known as FE2 method when the FEM is used at both macro and micro scales) and concurrent methods.

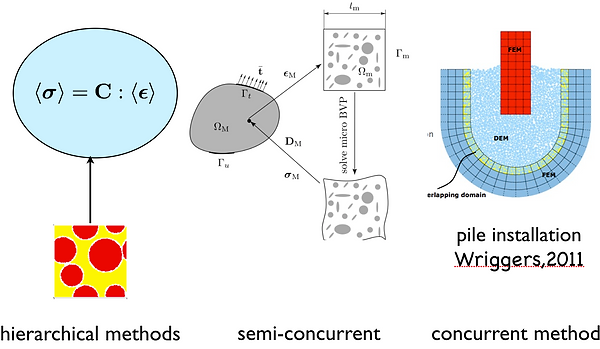
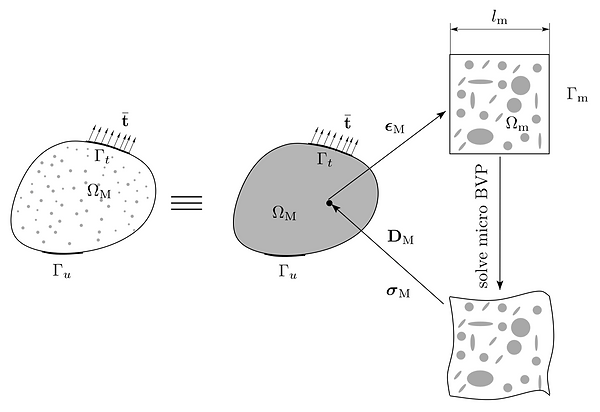
In a semi-concurrent multiscale method, a constitutive model is not needed at the macro-scale. Instead, the strain at a point (an integration point) is fed to a micro-scale BVP as boundary conditions. The micro BVP is solved, and the micro-stresses are averaged to obtain the corresponding macro-stress which is used in the macro internal force vector. A macro-material tangent matrix can also be defined based on micro-scale information.

Existence of Representative Volume Element (RVE) for softening materials
​
When it comes to softening materials, semi-concurrent multi-scale methods face a fundamental issue. That is the existence of an RVE which has been assumed to exist. However, when strain localisation is involved, as the localisation band has a constant width, when the RVE is larger, the averaged response is more brittle. To show this, we consider different concrete samples of size 10x10, 15x15 and 20x20 mm2. Each sample contains mortar, aggregates and ITZ. The damage of these samples is modelled using a gradient-enhanced damage model.
In order to solve this non-existence of RVE we proposed the so-called failure zone averaging scheme in which the averaging operations are performed over the evolving localisation band not oever the entire RVE domain. WIth this new average scheme, it has been shown that the averaged response is independent of the RVE size. In other words, there exists an RVE for softening materials if the failure zone averaging scheme is used.
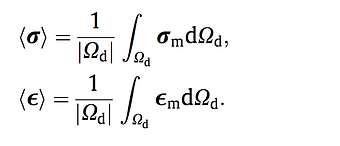
A discontinuous multi-scale method

Based on the failure zone averaging scheme, a discontinuous FE2 method was developed. The macro bulk material is described as an elastic material with homogenised material properties. When a failure criterion is met, a macro crack is inserted and the traction-separation law modelling the behaviour of that crack is obtained on the fly by going down to the micro-scale in a similar manner of the standard continuous FE2 method. The macro-crack is modelled using the eXtended Finite Element Method (XFEM).
 
A continuous-discontinuous multi-scale method
​
In the aforementioned discontinuous multiscale method, the nonlinear hardening stage at the micro-scale was not captured. To overcome this issue, a continuous-discontinuous multi-scale method was devised. This method combines the ideas of the continuous FE2 and discontinuous FE2 method. The scheme is illustrated in the figure.
​
​

References

 

  1. A. Karamnejad, V.P. Nguyen, and L.J. Sluys. A multi-scale rate dependent crack model for quasi-brittle heterogeneous materials. Engineering Fracture Mechanics, 104:96-113, 2013. link

  2. V.P. Nguyen, O. Lloberas-Valls, M. Stroeven, and L. J. Sluys. Computational homogenization for multiscale crack modelling. Implementational and computational aspects. International Journal for Numerical Methods in Engineering, 89(2):192-226, 2012. link

  3. V.P. Nguyen, M. Stroeven, and L. J. Sluys. An enhanced continuous-discontinuous multiscale method for modelling mode-I failure in random heterogeneous quasi-brittle materials. Engineering Fracture Mechanics, 79:78-102, 2012. link

  4. V.P. Nguyen, M. Stroeven, and L. J. Sluys. Multiscale continuous and discontinuous modelling of heterogeneous materials: A review on recent developments. Journal of Multiscale Modelling, 3(4):1-42, 2012. link

  5. V.P. Nguyen, M. Stroeven, and L. J. Sluys. Multiscale failure modelling of concrete: micromechanical modelling, discontinuous homogenization and parallel computations. Computer Methods in Applied Mechanics and Engineering, 201-204:139-156, 2012. link

  6. V.P. Nguyen, O. Lloberas-Valls, M. Stroeven, and L. J. Sluys. Homogenization-based multi- scale crack modelling: from micro-diffusive damage to macro-cracks. Computer Methods in Applied Mechanics and Engineering, 200(9-12):1220-1236, 2011. link

  7. V.P. Nguyen, O. Lloberas Valls, M. Stroeven, and L. J. Sluys. On the existence of representative volumes for softening quasi-brittle materials-A failure zone averaging scheme. Computer Methods in Applied Mechanics and Engineering, 199(45-48):3028-3038, 2010. link

A continuous-discontinuous rate-dependent multi-scale method
​
Finally, an extension to dynamic fracture is presented in Ref [1]. As can be seen in the figure next to the text, for each impact velocity, the macroscopic response is independent with the size of the RVE utilised. And rate-dependency of the material strength was captured.
​
​
bottom of page