top of page
This site was designed with the
.com
website builder. Create your website today.Start Now

What is Material Point Method?

 

The Material Point Method (MPM) is a hybrid mesh/particle method that is suitable for  discretizes a continuum body with a finite set of Lagrangian material points (or particles) in the original configuration that are tracked throughout the deformation process. The terms particle and material point will be used interchangeably throughout this manuscript. Since each material point contains a fixed amount of mass for all time, mass conservation is automatically satisfied. In MPM, the space where the simulated bodies might occupy is discretized by a finite element grid where the equation of balance of momentum is solved. This is in contrast to other meshfree/particle methods where the momentum equations are solved on the particles. In other words, particles do not interact with each other directly, rather the particle information is accumulated to the grid, where the equations of motion are integrated forward in time. This avoids the time-consuming neighbor search in the evaluation of the meshfree approximants/interpolants. The use of a grid allows the method to be quite scalable by eliminating the need for directly computing particle-particle interactions. The particles interact with other particles in the same body, with other solid bodies, or with fluids through a background grid. Most often, a fixed regular Cartesian grid is used throughout the simulation. This is the key difference between MPM and the updated Lagrange FEM and makes the method distortion-free. Note that the grid can be updated for every time step until it is distorted or even a completely new grid can be used. However this option was used very scarcely. 

​

We have recently published a book on this topic with Springer. Link:https://link.springer.com/book/9783031240690.

Sample movies:
gfgfdg.gif

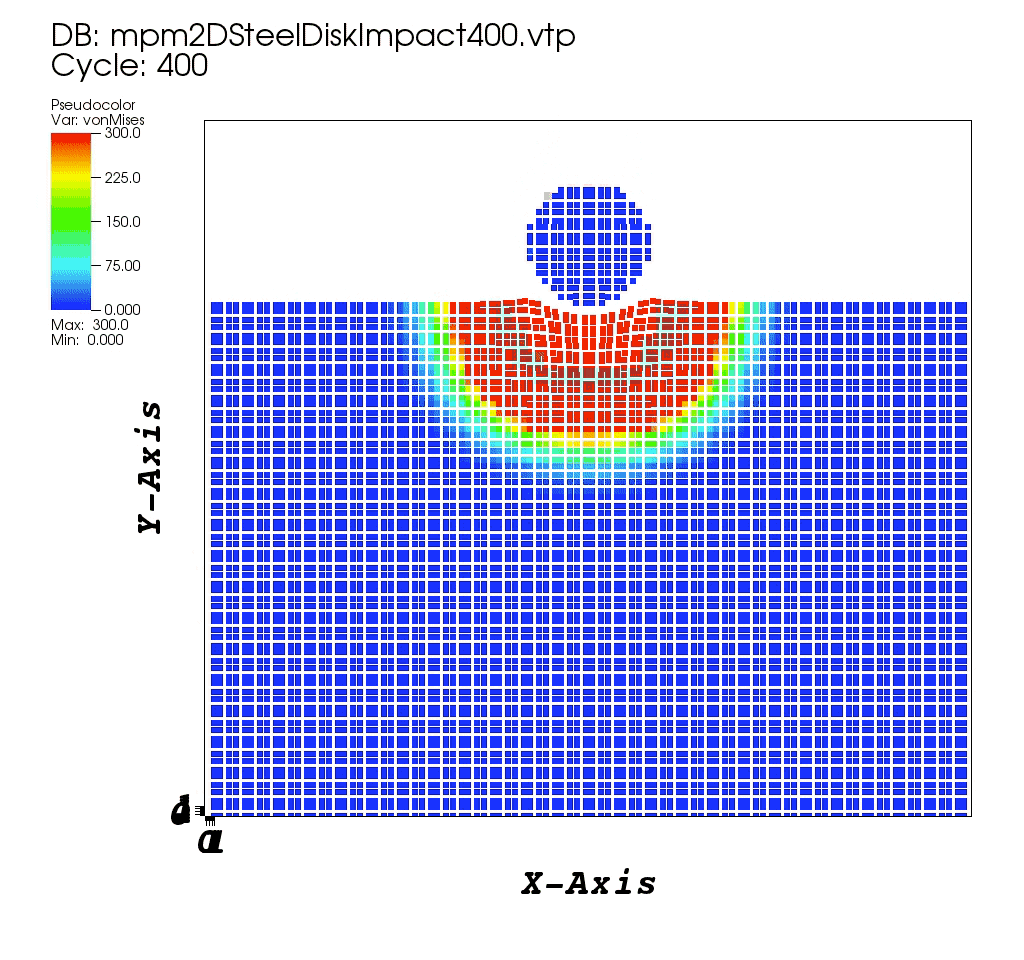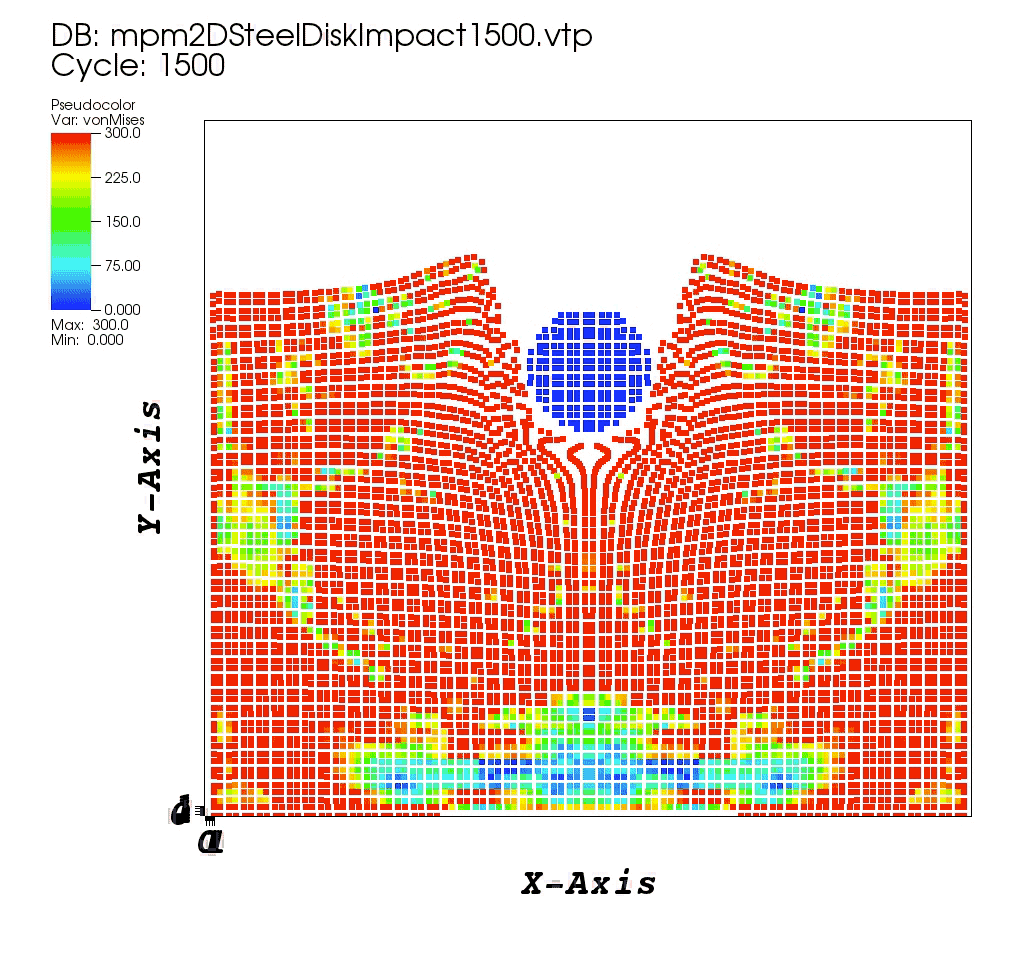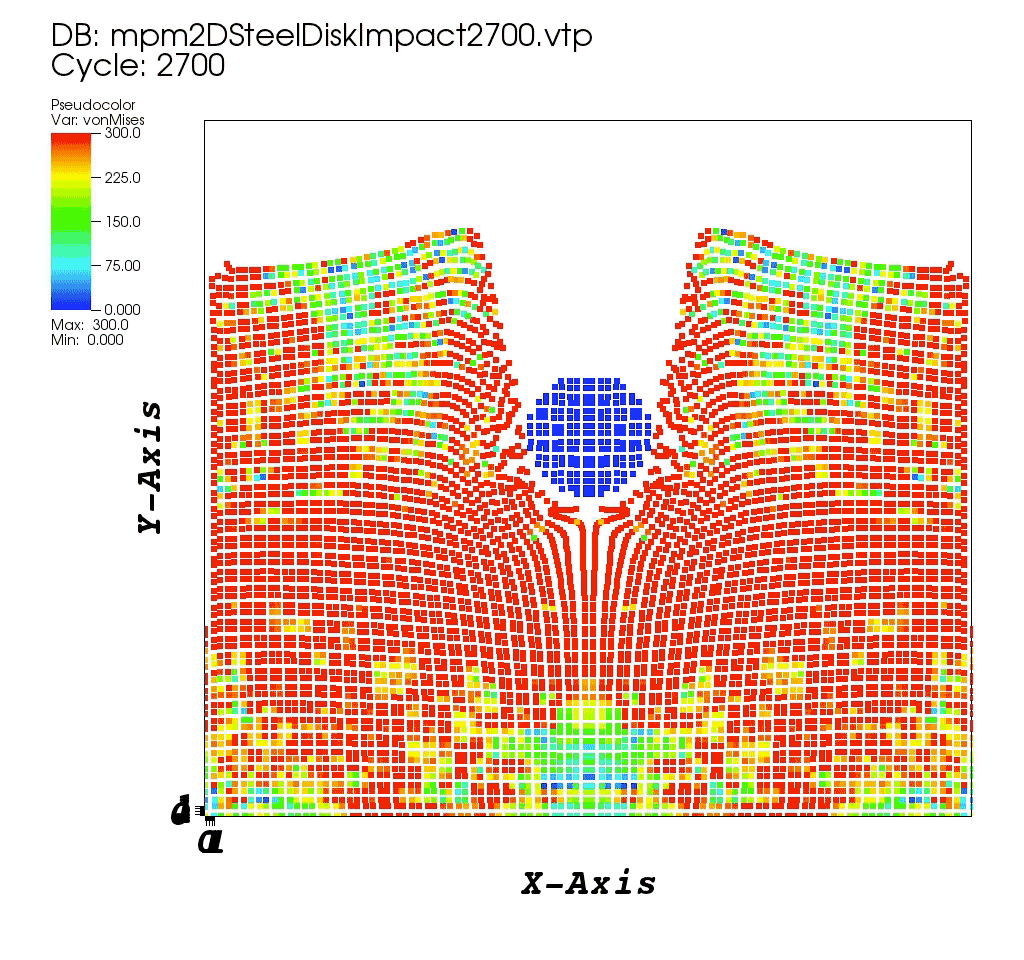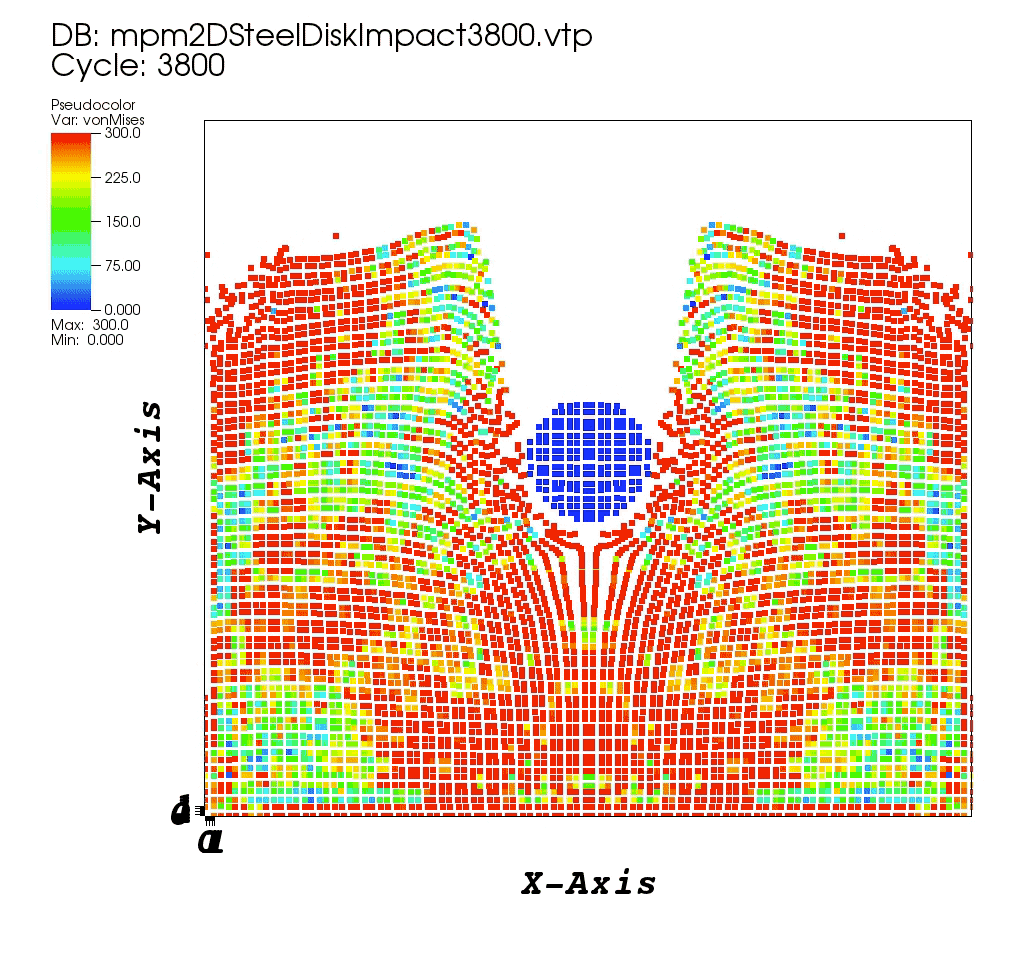
References

 

  1. D. Sulsky, Z. Chen, and H.L. Schreyer. A particle method for history-dependent materials. Computer Methods in Applied Mechanics and Engineering, 5:179–196, 1994. link

  2. VP Nguyen, A. de Vaucorbeil and S. Bordas. The Material Point Method: Theorey, Implementation and Applications. Springer, 2023.

  3. V.P. Nguyen, C.T. Nguyen, T. Rabczuk and S. Natarajan. On a family of Convected Particle Domain Interpolations in the Material Point Method. Finite Elements in Analysis and Design, 2016. link

  4. S. Sinai, V.P. Nguyen, C.T. Nguyen and S. Bordas. Programming the Material Point Method in Julia. Advances in Engineering Software, 2017. link

  5. S. Sinaie, T. D. Ngo, V.P. Nguyen and T. Rabczuk. Validation of the material point method for the simulation of thin-walled tubes under lateral comparison. Thin Walled Structures, 2018. link

  6. V.P. Nguyen. Material Point Method: Basic and Applications. link

  7. A. de Vaucorbeil, V.P. Nguyen, S. Sinaie and J. Y. Wu. Material point method after 25 years: theory, implementation, applications. link

  8. V.P. Nguyen, A. de Vaucorbeil, C.T. Nguyen, T.K. Mandal 2020. A generalized particle in cell method for explicit solid dynamics.  Computer Methods in Applied Mechanics and Engineering. link

  9. A. de Vaucorbeil, V. P. Nguyen and C. Hutchinson 2019. A Total-Lagrangian Material Point Method for solid mechanics problems involving large deformations. Computer Methods in Applied Mechanics and Engineering

  10. A. de Vaucorbeil, V. P. Nguyen, 2020. Modelling contacts with a total Lagrangian material point method. Computer Methods in Applied Mechanics and Engineering. link.​

  11. A. de Vaucorbeil, V. P. Nguyen and C. Nguyen-Thanh 2020. Karamelo: an open source parallel C++ package for the material point method. Computational Particle Mechanics, 2020

bottom of page