top of page
This site was designed with the
.com
website builder. Create your website today.Start Now
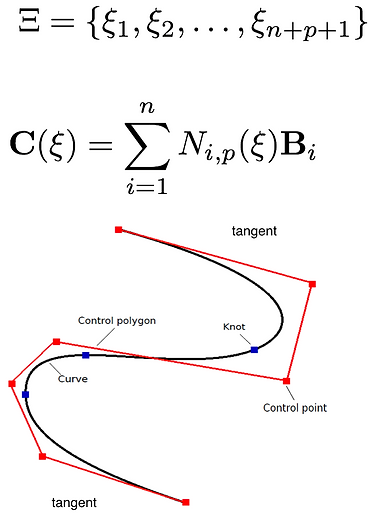
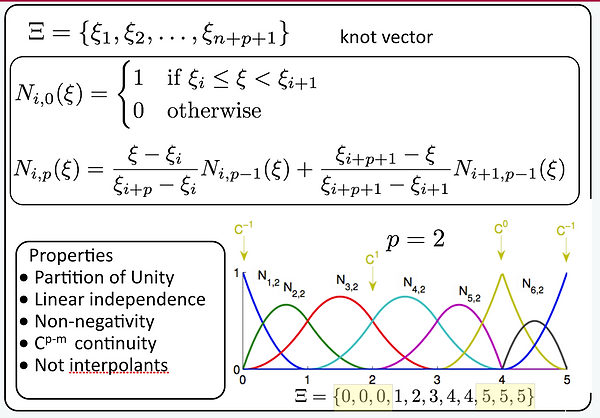
Isogeometric analysis (IGA) is a fundamental step forward in computational mechanics that offers the possibility of inte- grating methods for analysis into Computer Aided Design (CAD) tools and vice versa. The benefits of such an approach are evident, since the time taken from design to analysis is greatly reduced lead- ing to large savings in cost and time for industry. 
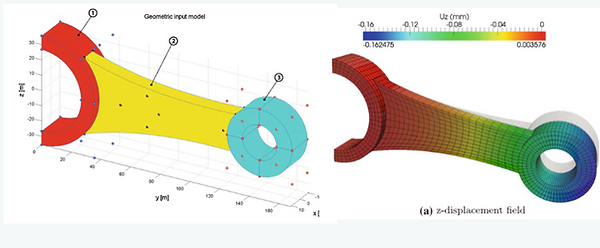
In Ref. 5, we developed a method to couple different NURBS patches of which parametrisation can be different. The method is based on the Nitsche method and it allows a flexible coupling of any patches. We applied our method to linear elasticity and free vibration analysis. 
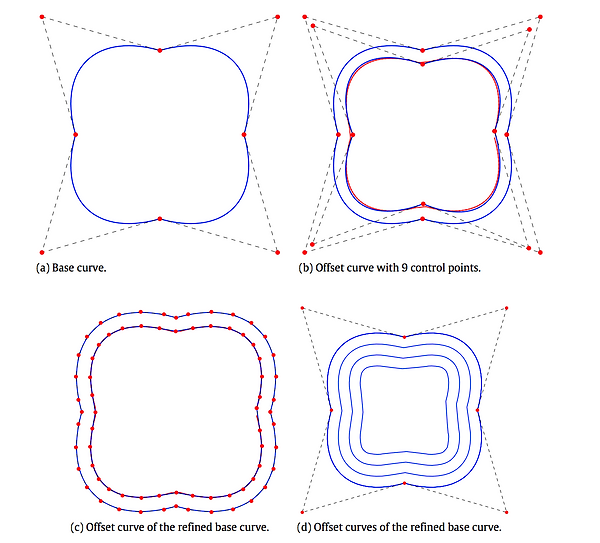
In Ref. 4, we devised a new method to build offset curves/surfaces. Our algorithm is different from existing ones in CAD in the sense that the base curve/surface and its offsets have the same parametrisation. This allows to build tensor-product NURBS volumes from these curves/surfaces. We applied our method to linear stress analysis of composite panels. 
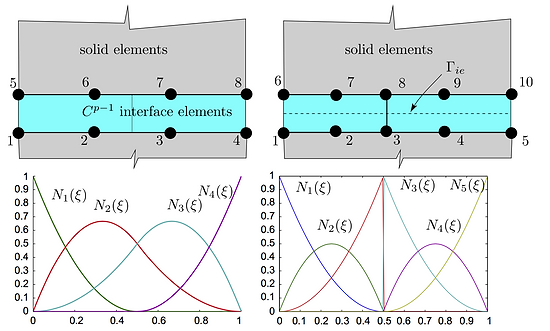
In Ref. 3, we proposed an isogeometric cohesive interface elements to model composite delamination often occurred in  composite laminates. The discontinuity lines are created straightforwardly using knot insertion algorithm. Therefore, the pre-processing is automatic and fast. The interface elements are smooth with any order and this results in a very efficient method to model delamination. Among many verified tests, a L-shape test is provided.  In Ref. 2, an easy introduction to isogeometric analysis was presented along with a Matlab code for linear elasticity, structural mechanics (beams,plates and shells). This paper is best suited for beginners to the field of IGA.

References

 

  1. T.J.R. Hughes, J.A. Cottrell, Y. Bazilevs, Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement, Computer Methods in Applied Mechanics and Engineering, Volume 194, Issues 39–41, 1 October 2005, Pages 4135-4195

  2. V.P. Nguyen, C. Anitescu, S. Bordas and T. Rabczuk. Isogeometric analysis: An overview and computer implementation aspects. Mathematics and Computers in Simulation, 117:89-116, 2014. link

  3. V.P. Nguyen, P. Kerfriden, and S. Bordas. Two- and three-dimensional isogeometric cohesive elements for composite delamination analysis. Composites Part B: engineering, 60:193-212, 2014. link

  4. V.P. Nguyen, P. Kerfriden, S.P.A. Bordas, and T. Rabczuk. Isogeometric analysis suitable trivariate NURBS representation of composite panels with a new offset algorithm. Computer Aided Design, 55:49-63, 2014. link

  5. V.P. Nguyen, P. Kerfriden, M. Brino, S. Bordas, and E. Bonisoli. Nitsche's method for two and three dimensional NURBS patch coupling. Computational Mechanics, 53(6):1163-1182, 2014. link.

  6. Nguyen-Xuan, T. Hoang, and V.P. Nguyen. An isogeometric analysis for elliptic homogenization problems. Computers and Mathematics with Applications, 67(9):1722-1741, 2014. link

bottom of page